FIGURATIVE TESSELLATION METHOD
Free online from my book "Parcelles d'infini"
published in French by Éditions Pour la Science, ISBN 2-84245-075-2, in 2005


Foreword
"The inventor has, all of a sudden, the distinct feeling
that the designs which he creates (...)
already existed before to have never been thought in the human brain.
Louis de BROGLIE
My song is really ended
when she looks to be made itself alone.
Georges BRASSENS
I have such sensations all the time when I am working on designs
for regular surface fillings.
It seems it is not I who am doing the creating,
but rather that the innocent
flat patches over which I am slaving
have their own will, and it is they which guide
the movement of my hand as I draw.
Maurits Cornelis ESCHER
"A long time ago, I chanced upon this domain in one of my wanderings I saw a high wall and a premonition of an enigma, something that might be hidden behind the wall, I climbed over
it with some difficulty. However, on the other side I landed in a wilderness and had to cut my way through with a great effort until - by a circuitous route - I came to the open gate, the open gate
of mathematics."
…
"I walk around all alone in this beautiful garden, which certainly does not belong only to me, but whose gate is open to everyone."
Maurits Cornelis ESCHER
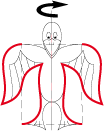
Periodic filling of a plan
This method, taken from my book "PARCELLES D’INFINI", offers a walk in the garden of the regular division of the plane that escher explored in many directions. This area may seem limited judging by the few artworks coming from others. I hope that what follows will make you realize that there are an infinite number of possible figurative motifs. And it is not just copying escher to make a periodic division of the plane.
… No more, for instance, than copying Jean-Pélerin* that makes a drawing in perspective.
And if, as I hope, you are inspired to do figurative ‘tiles’, throughout the following pages you will find how to give birth to them.
And when, after some difficulties, you successfully make one, you will experience a great feeling of joy and humility before this "PARCEL OF INFINITY".

*. Called the Viator. He wrote the first printed treatise on perspective, published in 1505.

1 IMITATING NATURE
There is so much art in nature
that very art consists to well heard and imitate it.
Jacques Bénigne BOSSUET
It is a sad thing to think that nature speaks
and that the human race is not listening.
Victor HUGO
 he laws of men are ephemeral, those of nature are eternal. Even if our
incursions on its paths will be always modest, this remains a great pleasure and a great honour that to be able to imagine plane variations on its own structures.
he laws of men are ephemeral, those of nature are eternal. Even if our
incursions on its paths will be always modest, this remains a great pleasure and a great honour that to be able to imagine plane variations on its own structures.The honeycombs of the bees, the fish scales or the sunflowers give us some fine examples of tessellations but it is especially the crystals that nature offers us to show us the way. We find in their structure the 17 symmetry groups allowing to repeat a pattern at infinity. But to draw figurative tessellations it would be preferable to create to us a both simpler and more appropriate classification. This is what we will do.

There are three regular polygons that can divide the plane periodically, these are:
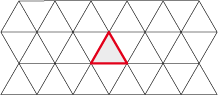
The triangle

The square
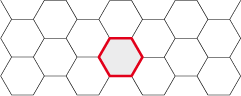
The hexagon
But fortunately, quantities of irregular polygons can also divide the plane periodically.
A few examples:
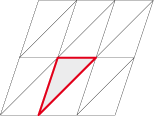
The triangle
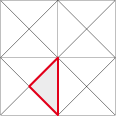
The right isosceles triangle
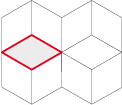
The rhomb 2 angles
120°
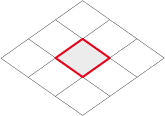
The rhomb
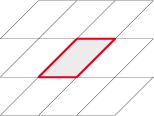
The parallelogram
The quadrilateral
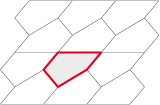
The pentagon 2 sides parallel and equal
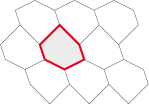
The hexagon 2 opposites sides
parallel
and equal, between
2 x 2 sides adjacent and equal
In addition, it is possible to replace the sides of all polygons dividing periodically the plane, by compensated deformations that does not alter their area.
Examples :

Translations of compensated deformations on parallelogram
Translations of compensated deformations on hexagon with opposites sides parallel

The multiplicity of achievable compensated deformations brings the amazing opportunity to give rise to an infinite number of figurative motifs.
.
Examples :
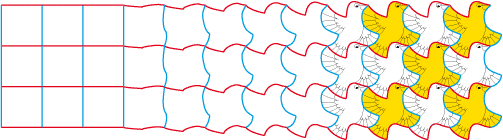
Progressive translations of compensated deformations on squares
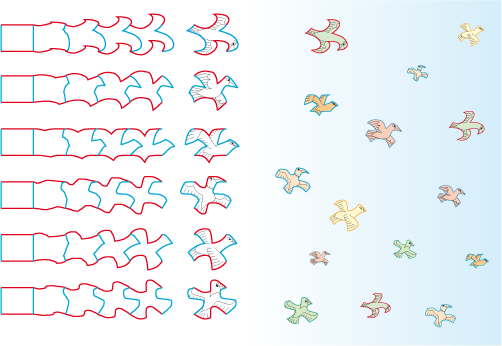
Transformations by translations of a same rectangle into six different birds
The base polygon having undergone compensated deformations is named tile.
Examples :
• Translations on a parallelogram:

Base polygon
Compensated deformation
Tile
• Translation on a square:
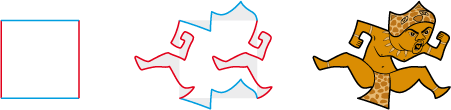
Base polygon
Compensated deformation
Tile
• Translation on a concave hexagon:
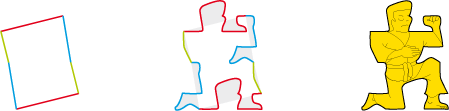
Base polygon
Compensated deformation
Tile
• Translation on a regular hexagon:
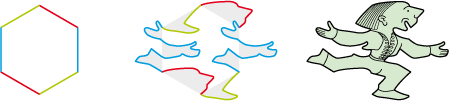
Base polygon
Compensated deformation
Tile
A squared paper facilitates the tracing of the tile.
Example :
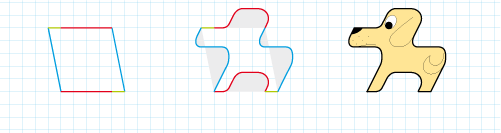
Base polygon (this is for us
a hexagon of which 2 x 2
sides are in prolongation)
Compensated deformations
Tile
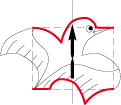
A set of tiles is named tessellation :

Lucky Blanchepatte, my dear gone dog

2 TRANSFORMING THE POLYGONS
The geometry is to fine arts
what grammar is to the art of the writer.
Guillaume APOLLINAIRE
More the art is controlled, limited, worked
and more it is free.
Igor STRAVINSKY
 rying to give birth to figurative motifs without geometric bases
gives very limited results. The polygons are the eggs from which will hatch a multitude of characters.
rying to give birth to figurative motifs without geometric bases
gives very limited results. The polygons are the eggs from which will hatch a multitude of characters.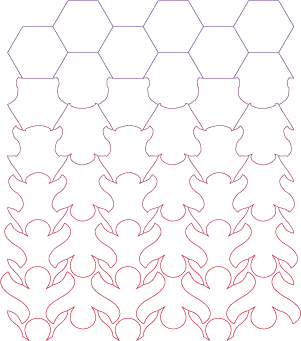
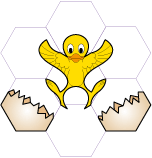

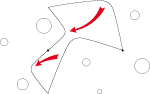
There are three possible deformations that can replace the sides of a polygon:
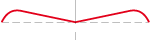
1. Any (as its name says):
side of polygon before deformation
side of polygon after deformation
symmetry axis
center of rotation

2. Axial (any deformation more its reflection in relation to an axis):
3. Rotatory (any deformation more its 180° rotation):

The deformation, of any or axial of a side must always be compensated by an identical deformation on another side. The rotatory deformation compensates itself. We call these compensations isometries.
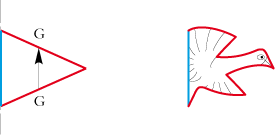
There are four types of isometries :
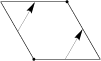
1. The translation is the simple rectilinear slide of one deformation:
2. The rotation rotation is either rotatory deformation or the pivoting of a deformation around a centre of rotation:
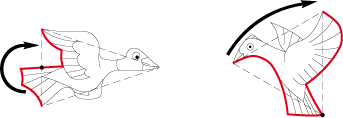

3. The glide reflection is the reflection of a deformation in relation to an axis, followed by a translation:
4. The symmetrie is the reflection of a deformation in relation to an axis:
Examples :
• Two translations on a parallelogram:

• A 180° rotation and another to 60° on an equilateral triangle:

• A glide reflection as well as a translation on a parallelogram:

• Two symmetrical slide reflections and an axial translation on hexagon:

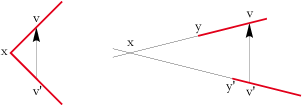
The glide reflection requires some clarification:
- The sides of the polygon may be adjacent (have a common end) or non-adjacent :
A polygon can have two glide reflections. In this case, their vectors axes are either parallel or perpendicular :
| adjacent | non-adjacent |
| Parallel | perpendicular |
The tracing of the
glide reflections
is particularly
simplified on
a sheet of
squared paper
Let L be the length of the sides of the polygon:

The v and v' points allow to trace the vector axis of the glide reflections. This vector axis indicates the axis of reflection as well as the direction and length of glide.
Example :

The base polygon of this bird is a concave pentagon having one rotatory side and 2 x 2 sides of perpendicular vectors axes.

ISOMETRIES
| DESIGNATIONS AND ABBREVIATIONS | CONDITIONS IN THE POLYGON | SIMPLIFIED REPRESENTATIONS |
| The translation | T | 2 sides parallel and equal |
The rotation | ||
- 180° | R2 | 1 any side |
- 120° | R3 | 2 sides equal and adjacent at 120° |
- 90° | R4 | 2 sides equal and adjacent at 90° |
- 60° | R6 | 2 sides equal and adjacent at 60° |
The glide reflection (If there are 2 in the polygon, we add ' to the 2nd) |
G | 2 equal sides |
The symmetry | S | 2 symmetrical sides |
There are four types of polygons that can divide the plane periodically:

| the triangle | the quadrilateral | the pentagon | the hexagon |
The systematic search for all possible combinations between the four isometries and the four types of polygons allows us to lead to a large amount of specific polygons of which we can
eliminate those unable to fill the plane.
Examples :
There then remains 81 specific polygons, called isohedral tiles, of
which we also eliminate those where the possibilities of obtaining figurative motif are too small:
- because having one or more rectilinear sides:
detained because
removed because
- because having central symmetry:
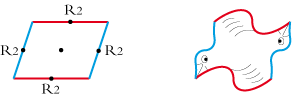
Ultimately, there remains 35 modal tiles; 35 parcels of infinity that the magician in you which lies dormant maybe, and will transform into a rabbit, butterfly or dove.

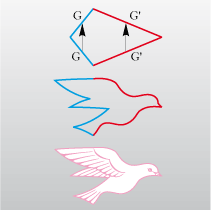
The need for a framework to this method should not let us forget that there are always opportunities to get out of the framework.
Examples :
• escher's splendid "Chinese" has two rectilinear sides:
• Half card-trick has a central axis of rotation:
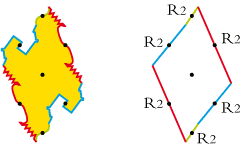

Here is its basic polygon:

• Same for the octopus:

3 ASSEMBLING THE TILES
It happens sometimes that a person (…)
feels born and grow in her, one day,
a desire very conscious to approach by the imagination,
infinity as close as possible
in the purest way.
Maurits Cornelis ESCHER
Hope nothing from human
if he works for his own life and not for eternity.
Antoine de SAINT-EXUPÉRY
The feeling of infinity
is the real human attribute.
Madame de STAËL
 ssembling the tiles, it is to arrange parcels of infinity on eternal
structures. Assembling the tiles, it is the privilege to play jigsaw puzzles with the universe.
ssembling the tiles, it is to arrange parcels of infinity on eternal
structures. Assembling the tiles, it is the privilege to play jigsaw puzzles with the universe.

Tiles similar to a modal tile can fit after rotation and/or glide reflection. They then have a
different orientation.
Examples :
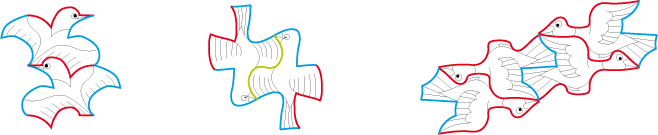
| Glide reflection | Rotation | Glide reflection + rotation |
This set of tiles can then similarly fit in turn by translation, and can then be continued to infinity :
| Type 1G | Type 2 | Type 2G |
All these similar tiles are the transformations of the base modal tile. The whole, we have seen, is called tessellation.

This round of lovers is just waiting to grow!
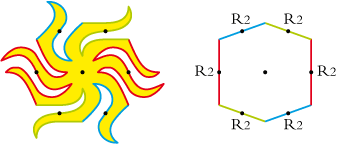
Visually, what characterises first a tessellation is the number of directions taken by the motifs. There are six possible directions, and therefore will be six original types.
Type 1 will have all its tiles in the same direction. Type 2 will have its tiles head to tail. Type 3 will have its tiles in three directions,
type 4 in four directions and type 6 in six directions.
Examples :
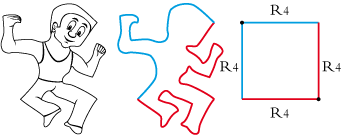
• Type 1, the athlete:
• Type 3, the lizard:

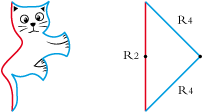
• Type 4, the kitten:


• Type 2, the siren:
• Type 6, the otary:


Then, the tessellations with one or two directions may have their motifs reflected. There will be also a type 1G (G for Glide reflexion) and a type 2G.
• Type 1G, the rooster:
• Type 2G, the dog:


Finally, tessellation types 1, 2, 3 and 4 may have their motifs symmetrical. We will have in addition type 1S, type 2S, type 3S and type 4S.
• Type 1S, the gorilla:
• Type 2S, the butterfly:


• Type 3S, the duck:
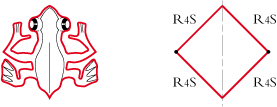
• Type 4S, the frog:


That is to say 11 types in totality, which will find themselves on 11 structures. In addition, these 11 types have subtypes classified according to their basic polygon. In total, we meet again the 35 modal tiles of the previous chapter.
• The base polygon of the kitten is a right isosceles triangle. We will designate it by the isometries of the sides, that is to say R2 R4 R4:
• The one of the frog is a square. Designation R4S R4S R4S R4S:
Now here are the designations of basic polygons for:
• the athlete: T T T T T T
• the siren: R2 R2 R2
• the lizard : R3 R3 R3 R3
• the otary : R2 R6 R6
• the rooster : T G T G
• the dog: R2 G G
• the gorilla: T GS GS T GS GS
• the butterfly: T R2S R2S T R2S R2S
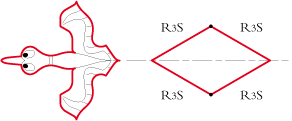
• The one of the duck is a rhomb with two angles of 120°. We will refer it by R3S R3S R3S R3S because the sides are both of 3 rotations and symmetries:
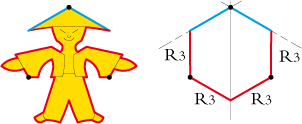
The base polygon of the 'madman' is a regular hexagon. Designation R3 R3 R3 R3 R3 R3:
The use of isometric paper is ideal for tracing tiles with isometries of rotations 3 or 6.
• The base polygon of the "Li'l strong man" is a square. We will designate it by R4 R4 R4 R4:
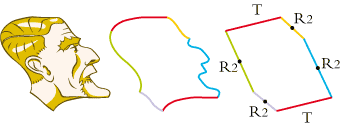
• The one of escher (Oh yes! even the escher's profile is a tile!) is a hexagon. Designation T R2 R2 T R2 R2:



4 TRACING THE STRUCTURES
If there is a trick, it is even stronger!
MYR et MYROSKA
All things, near or far,
secretly are connected to each other
and you cannot touch a flower without disturbing a star.
Francis Joseph THOMPSON
 he structures are similar to the scenes of magic theatres, in
that they contain all the secrets needed for representation. To know these secrets disenchants only the fool.
he structures are similar to the scenes of magic theatres, in
that they contain all the secrets needed for representation. To know these secrets disenchants only the fool.

We have seen that there are 11 structures, but the crystallographers count 17 symmetry groups. In fact, the six missing groups do not allow us to
create unique motifs. We will indicate all the same the 6 groups of structures that do not allow to make unique motifs, this after the first 11 groups
The structures are represented using the following elements:
- center of rotation : •
- symmetry axis : ———— — ——— — ———
- axis of glide reflection : ——————————
| TYPE 2G (pgg) Rotation 180° + glide reflexion + translation | Structure + base polygon and its transformations before translations | Example of base tile |
Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
b (IH53) Quadrilateral R2 R2 G G
36 / 412 / 77 / 98 / 116
The symmetry group used is that of the International Tables for x-ray crystallography.
The isohedral type defined is the
one as given by B. Grünbaum and G. C. Shephard in their book Tilings and Patterns.
When we have several kinds of transformations before
translation as in the present case, we try the first: this gives us two tiles. Then we make:
- either the transformation of the two tile set
(top example);
- either the transformation of each of the two tiles separately (example below with concave tiles).
The small numbers indicate the angle of rotation (2 = 180°, 3 = 120°, 4 = 90°, 6 = 60°).
The structure of type 1 will be vacant because
it contains only translations.
Nineteen basic polygons may be concave. These are: 1b, 1Gb, 1Gc, 1Gd, 1Sb, 2b, 2d, 2e, 2Gb, 2Gc, 2Ge, 2Gf, 2Gg, 2Gh, 2Sb, 2Sc, 3b, 4c et 6d. Exemple :
The figures indicate the number of adjacent vertices.
The 35 types of tessellations will be represented by 35 birds.
All isohedral tessellations can be coloured with a minimum of two or three colors. If all adjacent vertices are of even numbers, two colors are sufficient. If there are vertices of odd numbers, three colors are needed.
| TYPE 1 (p1) Translations |
Structure + base polygon before translations | Example of base tile | Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH41) Parallelogram T T T T
38 / 472 / 482 / 492 / 502
/ 522 / 73 / 74 / 80 / 105 / 106 / 127 / 128
b (IH1) Hexagon T T T T T T
182 / 222 / 272 / 282
/ 292 / 302 / 722 / 822 / 842 / 872 / 922 / 1112 / 1122 / 1132
/ 1142 / 1202 / 1212 / 1292
| TYPE 1G (pg) Glide reflection + translations |
Structure + base polygon and its transformation before translations | Example of base tile | Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH43) Parallelogram T G T G
31 / 32 / 7112 / 97 / 108 / 109
b (IH44) Kite * G G G' G'
19 / 62 / 66 / 67 / 762 / 96 / 102 / A13
*. A kite is a quadrilateral whose one diagonal is perpendicular to each other in the middle).
c (IH2) Hexagon T G G T G' G'
242 / 262 / 78 / 1102 / 1262 / 1302
d (IH3) Hexagon T G G' T G' G
17 / 342 / 612 / 632
| TYPE 1S (cm) Translations |
Structure + base polygon before translations | Example of base tile | Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH68) Rhomb GS GS G'S G'S *
91 / A14
*. The sides with glide reflection being symmetrical, they are also and necessarily translations.
b (IH12) Hexagone T GS GS T G'S G'S *
A1
*. The sides with glide reflection being symmetrical, they are also and necessarily translations.
| TYPE 2 (p2) Rotation 180° + translations |
Structure + base polygon and its transformation before translations | Example of base tile | Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH84) Triangle R2 R2 R2
51 / 95
b (IH46) Quadrilateral R2 R2 R2 R2
9 / 88 / 90 / 93
c (IH47) Parallelogram T R2 T R2
75 / 1152
d (IH23) Pentagon T R2 T R2 R2
escher did not make tessellations of this type
e (IH4) Hexagon T R2 R2 T R2 R2
1 / 5 / 6 / 7 / 8 / 11 / A12
| TYPE 2G (pgg) Rotation 180° + réflexion glissée + translations |
Structure + base polygon and its transformations before translations | Example of base tile |
Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH86) Isoceles triangle R2 G G
escher did not make tessellations of this type
b (IH53) Quadrilateral R2 R2 G G
36 / 412 / 77 / 98 / 116
c (IH51) Quadrilateral R2 G R2 G
33 / 107 / 124
d (IH52) Rectangle G G' G G'
39 / 682
e (IH25) Pentagon T R2 T G G
f (IH27) Pentagon R2 G G' G G'
16 / 462 / 592 / 602
g (IH5) Hexagon T R2 R2 T G G
10 / 582
h (IH6) Hexagon R2 G R2 G' G G'
2
| TYPE 2S (pmg) Rotation 180° + translations |
Structure + base polygon and its transformation before translations | Example of base tile | Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH66) Rectangle T R2S T R2S *
40 / 117
*. The sides with rotation 2 being symmetrical, they are also and necessarily glide reflections.
b (IH69) Kite R2S R2S R2S R2S *
37 / 89
*. The sides with rotation 2 being symmetrical, they are also and necessarily glide reflections.
c (IH13) Hexagon T R2S R2S T R2S R2S *
escher did not make tessellations of this type
*. The sides with rotation 2 being symmetrical, they are also and necessarily glide reflections.
| TYPE 3 (p3) 2 rotations 120° + translations |
Structure + base polygon and its transformations before translations | Example of base tile |
Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH33) Rhomb R3 R3 R3 R3
escher did not make tessellations of this type
b (IH7) Hexagon R3 R3 R3 R3 R3 R3
21 / 25 / 432
| TYPE 3S (p31m) 2 rotations 120° + translations |
Structure + base polygon and its transformations before translations | Example of base tile |
Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH36) Rhomb R3S R3S R3S R3S *
532 / 542 / 103 / 123
*. The sides with rotation 3 being symmetrical, they are also and necessarily glide reflections.
| TYPE 4 (p4) 3 rotations 90° + translations |
Structure + base polygon and its transformations before translations | Example of base tile |
Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH79) Right isoceles triangle R2 R4 R4
35 / 118 / 119
b (IH55) Square R4 R4 R4 R4
15 / 23 / 104
c (IH28) Pentagon R2 R4 R4 R4 R4
14 / 20 / 423,5
| TYPE 4S (p4g) 3 rotations 90° + translations |
Structure + base polygon and its transformations before translations | Example of base tile |
Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH71) Square R4S R4S R4S R4S*
13 / 452 / 86 / 122 / 125
*. The sides with rotation 4 being symmetrical, they are also and necessarily glide reflections.
| TYPE 6 (p6) Rotations 180°° + 2 rotations 120° + translat. |
Structure + base polygon and its transformations before translations | Example of base tile |
Example of figurative tile | Example of arrowhead and colored tessellation (minimum of colors) |
a (IH88) Equilateral triangle R2 R6 R6
44 / 94 / 99 / 100
b (IH39) Isoceles triangle R2 R3 R3
escher did not make tessellations of this type
c (IH31) Kite R3 R3 R6 R6
55 / 56
c (IH21) Pentagon R2 R3 R3 R6 R6
572 / 70 / 79
The six groups of symmetry do not allow us to make unique motifs:
| Designation | Structure | Example of figurative tile | Designation | Structure | Example of figurative tile |
pm
(Minimum
2 motifs)
p3m1
(Minimum
3 motifs)
cmm
(Minimum
2 motifs)
p4m
(Minimum
3 motifs)
pmm
(Minimum
3 motifs)
p6m
(Minimum
3 motifs)
The 35
base
polygons

5 USING BASIC POLYGONS
Imagination is more important than knowledge.
Albert EINSTEIN
The reason, it is the intelligence in exercise;
the imagination, it is the intelligence in erection.
Victor HUGO
 ou have the quill and the parchment. You have taken
knowledge of the structures secrets. You now need to appeal to the most important: your imagination. If on an old decrepit wall you see figures appearing more or less
of a fantasy nature, you have a good chance of success.
ou have the quill and the parchment. You have taken
knowledge of the structures secrets. You now need to appeal to the most important: your imagination. If on an old decrepit wall you see figures appearing more or less
of a fantasy nature, you have a good chance of success.When designing you can randomly choose a basic polygon and trace compensated deformations until you get a rough outline of motif. Or you may already have an
idea of the motif to draw, trace it roughly, and adapt on it the type of best suited basic polygon and go back over the compensated deformations.
Of course, you will need to use a lot of the eraser before succeeding with a figurative tile.
Often your motif will be only half successful and so you will need to
start over again..
But if really you get nothing satisfying, all is not lost. With the help of your computer, trace again your failed tile. Inside your tile add some motifs not connected,
then select all and give a background gradient to all these traces, in the rainbow or tropical sunset style. It only remains to you to baptise the whole of a silly
name and you just created a worthy representative of abstract art!

Now that you know how to work the structures, the summary of the previous 35 basic polygons will help you to give birth to figurative tiles. Your hardware: squared paper, isometric paper for types 3 and 6, a pencil and an eraser. That's all! When you will want to multiply the tiles to make tessellations, a computer with a drawing program will be convenient. But that is not required, do not forget that escher drew all his tilings by hand. Tessellation software like that of Kevin Lee (designer of TesselManiac) will also provide you with valuable assistance for the creation of tiles.
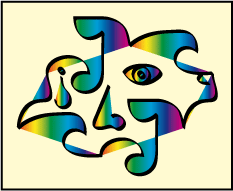
Hexus
(Abstract art!) type 1b
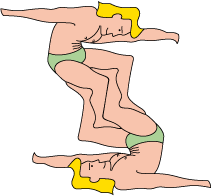
Elbow to elbow
Impossible icarian antipodists
type 2c

Wrong way

Samson's sleep
(Modern art!) type 2c

Beware… fir!

Jealous
After this little interlude of more or less successful tiles, we come back to our base polygons.
• Let us take a square of type 1Ga. Trace a few broken lines on two adjacent sides (a). Then let us transfer them on the two other sides using a translation and a glide reflection (b). Let us study the resulting figure: It vaguely has a look of a little man. Let us reduce the left arm, this augments the right arm (c):
Let us modify the left leg, and that improves the definition of the right arm and the right leg (d). Let us refine the exterior details taking account both of what would be the ideal line on one side and what would be the one of its isometry (e). Now let us draw the interior details of the little man. One realizes that we can still improve certain outside line elements (f).
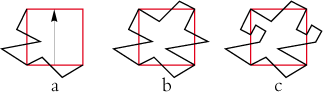
Now just realize of what we made: We have transformed a rigid square into a young boy who runs happily on our sheet of paper!
• Let us now take a rectangle, of type 1Ga, and draw a few lines. We soon get the silhouette of a marching service man:
But his silhouette is leaning forward. Transforming the base rectangle into a parallelogram will enable us to straighten it out:
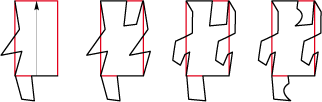
And behold, from a rectangle at the beginning, we get a valiant service man who parades proudly below.
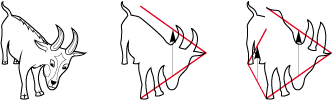
• In fact, a good number of drawings of figurative tiles begin by being... some drawings! Let us take for example the goat below. Let us examine it. It appears clear that there is a possibility of a glide reflection between the front legs and horns:
Then maybe another between a hind leg and the tail. It then only remains to adapt the glide reflections into a kite type 1 Gb:
And here is a brave little goat that comes down from the mountain:
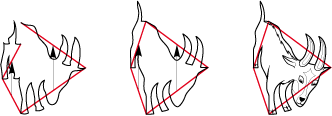
After these three examples, perhaps it seems easy to you to draw figurative motifs. Don't believe it; you need to try and try again, hundred times on the drawing board start your work again.
• Let us take again a square of type 1Ga and try a few lines: After the transformation of the square into a rectangle and then a parallelogram there appears an Indian, the hand raised as a sign of peace:
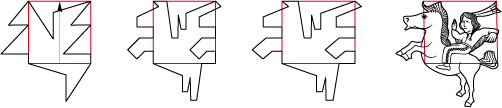
• After the Indians, here are the cowboys with as base polygon a hexagon of type 1Gc:
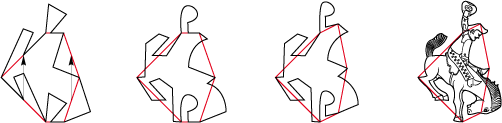
• Let us find again the historic figure of the rodeo cowboy in a concave hexagon type 1Gd:

You will notice that the hat is detached from the rider and his horse. We have there, in fact, a tile composed of two subdivided tiles (see chapter Dividing the tiles).
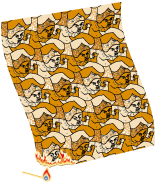
• Let us stay in America with the creator of rockabilly, Elvis himself, in this regular hexagon of type 1Gc:
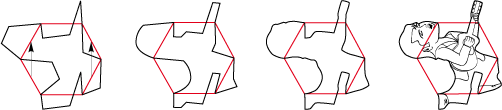
• The rhomb type 1Sa is suitable to appear as the silhouette of a bear:

• But if we lean the bear, the rhomb turns into a parallelogram of type 1a:

• And if the bear starts to dance, the base polygon becomes a kite type 1 Gb:

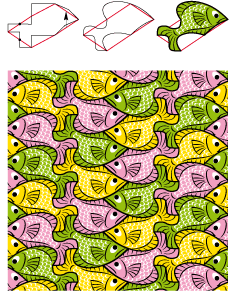
• The rectangle of type 2Gd easily turns itself into an undulating fish and could make a nice bathroom tiling:

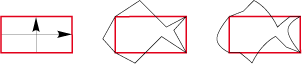

• From a sharp triangle of type 2 is born the pretty curves of a pretty girl:
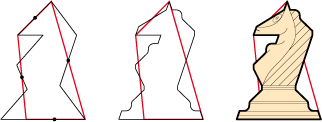
• The chess piece horse is developed from a quadrilateral of type 2b:
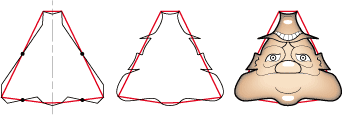
• This big good guy splendidly fills a hexagon of type 2Sc:
• This parallelogram of type 2b turns itself into a quadrilateral to reveal a judo player at the heart of the action:
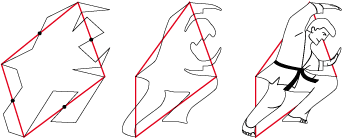
But he has maybe a hidden face...
• Also in action is this acrobat monkey born from a concave pentagon type 2Ge:
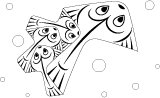
• A type 2Gg hexagon is at the base polygon of the fish below.
But only by its contours, as details of half of the fishes - which should be upside down - was
drawn right way up.
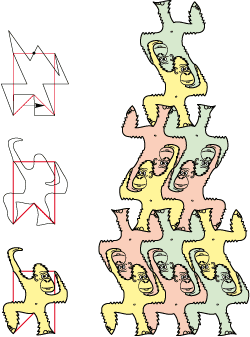

• This inflatable lizard is very convenient to be stored on the beach.
Its underlying polygon is a hexagon of type 2Gh:
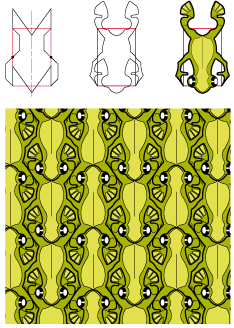
• The green tree frog can come and go in a rectangle of type 2Sa:
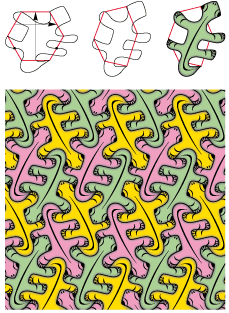
• Apart from its ventral fins, the angelfish fits perfectly to a kite type 2Sb:
• This square of type 4b may give birth to a crested bird:

• You can cut the jumping jack below and assemble it:
Perhaps you notice that with the arms and legs in the air this one can also be born from a rhomb type 3Sa. So we can draw its transformations and thus constitute us with an army of jumping jacks !
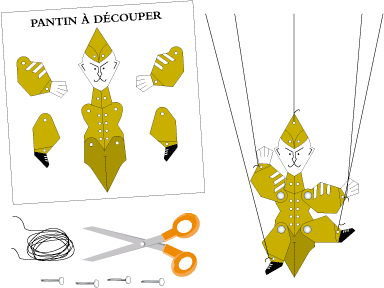


6 DIVIDING THE TILES
People never divert themself so well that at the pursuit of eternity.
Jean GIONO
If you want to progress towards infinity,
explore the finite in all directions.
Johann Wolfgang von GOETHE
 s cells divide themselves to multiply, why not make tiles
to go two by two, see three by three or even more, to tessellate infinity?
s cells divide themselves to multiply, why not make tiles
to go two by two, see three by three or even more, to tessellate infinity?The tessellation with this hexagon will give the figure below. Three colors are needed:


The tiles of all the types that we have seen can be divided into as many subdivided tiles as we want.
Take for example a hexagon with opposite parallel
sides of type 1 b:

Let us divide the hexagon in several ways:
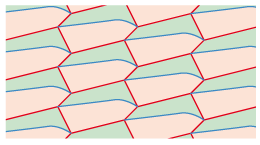
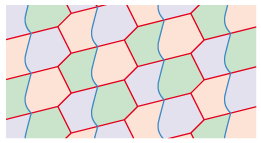
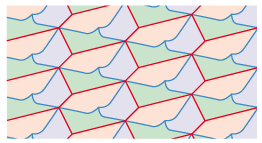
In fact we can divide the base tile in as many different ways as we wish.
Division causes changes in the vertices, and so in the minimum
number of colors. We have seen that if all adjacent vertices of an isohedral paving are of even numbers, two colors are sufficient, and that if there are vertices in odd
numbers, three colors are required.
It is not the same for the subdivided tiles, as that may require up to four colors.
| Example type 1b | Example type 3b |
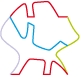
• Here is a tile type 2Gc which resembles nothing much:
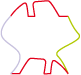
But when it is divided into two it reveals a fish and a lizard:
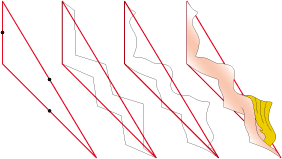
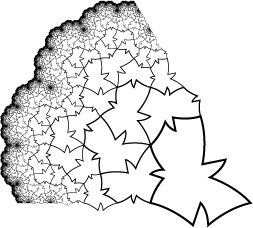
• During a walk, pick up a leaf. Draw its outline:
Copy a third and a fourth still making them coinciding with another vertex.
With tracing paper draw a second leaf by coinciding two of the vertices:
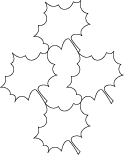
With this method you can have the chance of seeing appearing a rabbit among the autumn leaves or a dove among the stars.

• Here are those of the Inaccessible Star: :
• Here are the base polygon and the base tile of the 'rabbit among the autumn leaves':


You may have noticed that the dove and the star above do not have quite the same outline that the dove at the bottom and the star of the top of the drawing does. It is this appearance/disappearance style of drawing dear to escher that allows these approximations. These matters are sometimes even more pronounced in the drawings that follow.

Here is the base tile of 'Two Elements':
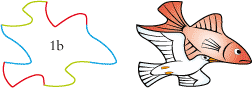
• This bird and this fish would be perfect in an appearance/disappearance style drawing, but the result would have been too close to escher’s Sky and Water.
• Here is the base tile of Child's Eye View: :
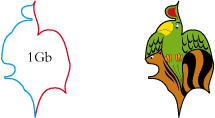
This child look that might be the one of Albert Flocon – the brilliant engraver artist - which sets out the rules of the curvilinear perspective, this one giving a more logical and exciting image than the classic perspective for which we have structured space with straight lines that make it sad.
"Learned since childhood, familiar for four centuries,
the traditional image is credited finally for the real image.
It is perhaps an
imposture…"
Albert FLOCON / André BARRE
La Perspective curviligne
And now, if we divide a few tiles into several lizards:
• First of all here is the base tile of Lizards Squares, divided into three lizards including two that are identical:


• And here is the one of the opposite tessellation:

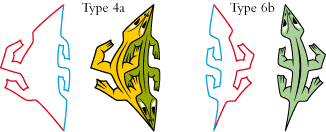
• The Rose with Lizards is constructed by using tiles of type 4a and 6b between which we have made a few adaptations.

• The drawing below has a type 3b base tile divided into four lizards:

7 TESSELLATING WITH WORDS
The words are chump change of thought.
There are big talkers who pay us in dimes parts.
Others, on the contrary, give only golden louis.
Jules RENARD
The art is beautiful when the hand, head and heart work together.
John RUSKIN
 et us ask ourselves the question: could the motifs be other
things than familiar figures, such as animals, objects or humans while still having recognizable contours? Well yes, of course! There are the
characteres; these signs that men have imagined to communicate and which are, moreover, already in two dimensions.
et us ask ourselves the question: could the motifs be other
things than familiar figures, such as animals, objects or humans while still having recognizable contours? Well yes, of course! There are the
characteres; these signs that men have imagined to communicate and which are, moreover, already in two dimensions.And even better: there are character sets that are the words and who have as well a specific meaning. We can choose a word for what or who it represents, for its value to us. We can draw it, work it, perfect it... love it as much as a poet.
Why escher did not make any tessellations with words remains a great mystery. The way has been indicated in a book by Scott Kim. Its title? Inversions. A unique book, at the border between calligraphy and mathematics. We find in, among other wonders, the word "figure" in white on a black background and which the space between letters gradually turns into black letters on a white background, again forming the word "figure" in negative. There is also the word "Lester", with the space between the letters forming the word "Pearl" (these are the Kim's parents). These are not tessellations but it is already good way along.
It was tempting to go this way and make words in Kim's style. It was exciting to go at the end of the road and realize an old childhood dream: to make tessellations with words. And if possible with words dear to my heart..

We have seen that it is easy to divide a tile in two, three or more parts. Well, a tile-word is only the equivalent of a tile divided into as many subdivided tiles it contains letters, accents or dot on the i. It is the assembling of the base tile with its transformations and then the coloring that allows us to read the word in different colors.
• There are no tessellations in the opposite example. But we could cut type 4b tiles like the one below:

• Among several early attempts of tessellations with words, here is this one at right:
An inconclusive attempt. But the result is interesting all the same.

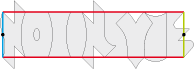
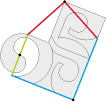
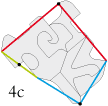
• Honor to the good master. Here is the type 4c base tile used for escher Pavage (this means escher Tessellation in French):
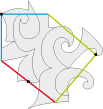
The transformations of this base tile allow us to read the word "escher" in four directions.
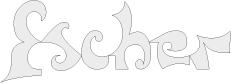
• We find again this tile-word in decoration around escher's portrait.
• Let us take again the tile-word "escher". And let us color it as below. We see then to appear… Le Jardin d'escher
(The garden of escher in French).
Tiling example :


• Here is the type 2e base tile of Kim :
• Translation axes, rotation axes, symmetry axes, glide-reflection axes; the axes are present in all tessellations. Below you will find the type 6a base tile (equilateral triangle) of Axes:
The transformations of this base tile allow us to read the word "Kim" in two directions.
• En route to a ride to the Étoiles (Stars in French). Here is the used type 6a base tile:
• Then here is the type 2c base tile of Inversion a particularly dear word to Scott Kim:

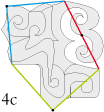
• Honor to the natural order, here is the type 4c base tile used for L'Ordre et le Chaos (The Order & the Chaos):
• Yet on the contrary, here is the type 1b base tile of Paradoxe Jour / Nuit (Paradox Day / Night):
• Of course, it must have a name of musician. To quote geniuses such as Bach or Mozart would certainly make a good impression... but it would not reflect my taste for good old Country music, music that I love and which brings me joy and satisfaction. And do not tell me that there are no geniuses in Country music. Merle Travis not only was one, but even more was a multi-talented genius. He excelled both as author, composer, cartoonist, watchmaker, historian, actor, writer, naturalist, impersonator, designer of guitars, singer and of course as a virtuoso guitarist. We are indebted to him for the guitar style that bears his name, the Travis-pickin’. A style in which the accompaniment, bass and melody are played at the same time.
Here is the base tile of Travis:


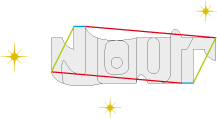
• Brassens... Ah, Brassens! The man with a hundred masterpieces. The perfectionist of the "beautiful language" and chosen expression. The wonderful artisan engraver of words. That the word "Brassens" extends to infinity.

• Depending on that it is white or black, the magic indicates either the art of producing some wonderful effects that are due to natural causes, or the sordid
mystification by which some people claim to produce supernatural effects by the intervention of the spirits.
Here is the type 1a base tile used in Magie blanche / Magie noire (White Magic / Black Magic):
• Among the artists of white magic, Gérard Majax is a worthy representative of them, which does not hesitate to work against the phonies of illusion, the
supposedly owners of extraordinary powers and others twisters of teaspoons.
Here is his type 1b base tile:
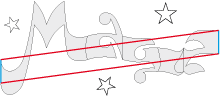
• Of course, here is the base tile of the unavoidable Infini (Infinity):
• Then here is the type 2e base tile of Pavé (Tile!). First in two tones then into only one gradient tone.

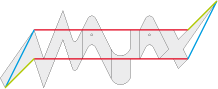
• This type 6a almost triangular tile is the one of Victorian tessellation:
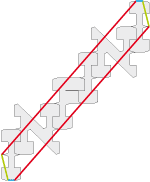
• If there is a name deserving to tessellate the infinite, it is that of "Einstein". Here is the used type 2e base tile:

"The joy to contemplate and understand,
this is the language that nature inclines to me."
Albert EINSTEIN
How I see the world
• Erno Rubik is the inventor of the Rubik's Cube, the most diabolical of all puzzles. Here is the type 6d base tile of Rubik's Cube:
• Where is the border between good and evil (Bien et Mal)? Here is the type 1b base tile of Frontière (Boundary):
• Here is the one of Nicolas Pavage 2, type 3a:
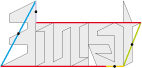
• It is, of course, tempting to tessellate with its own name. Here is the type 1b base tile of Nicolas :
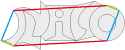
• Finally with words, here is again "Infini" (Infinity) written in a manner that with its transformation by rotation fills exactly a rectangle. We can then assemble the words like bricks.
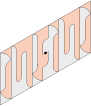
• Then the same word in a parallelogram:


8 DISTORTING THE STRUCTURES
What is worth to be done is worth to be well done.
Nicolas POUSSIN
The harmony of proportions satisfies the senses.
Saint Thomas d'AQUIN
 hat is better is the enemy of what is good. But the good is
often the friend of what is mediocrity! Let us try to find the better by distorting the structures for dress up concentric circles, spirals, perspective or volume effects.
This will allow us to discover new horizons full of wonderful harmonies.
hat is better is the enemy of what is good. But the good is
often the friend of what is mediocrity! Let us try to find the better by distorting the structures for dress up concentric circles, spirals, perspective or volume effects.
This will allow us to discover new horizons full of wonderful harmonies.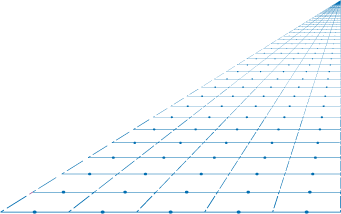

Opposite, here is for example what produce a type 2S structure on a perspective:

• Here is the tessellation (type 2Gb) of Cascade:
• Here is the one of Miel (Honey), type 2Sb:


• Here is the one of Plouf ! (splash!) type 1Sb:
• The one of Spirale d'infini (Spiral of infinity), type 2d:

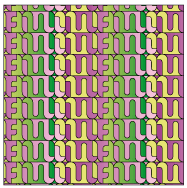
Hello…
It's me
again!
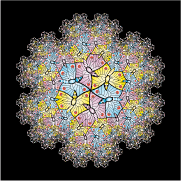
• Opposite here is the original tessellation of type 6b which served for Cercles (Circles). Nine colors are required so as not to have
intersecting circles of lizards.

• This same tessellation also served for the Icosaèdre aux lézards (Icosahedron with Lizards) below. An icosahedron is a polyhedron with
twenty equilateral triangles for faces. Six colors are necessary to obtain a harmonious distribution. There are five lizards’ noses by the vertex.
• How to put seven lizards' noses by vertex? It is impossible on the normal plane, but not on a hyperbolic disk. The lizards are then reduced to infinity on a circular limit. To ensure the same color to the lizards which follow each other and that two columns of the same color do not intersect, seven colors are needed. In fact, in the disk, if one considers the colors, there are not two identical lizards.

9 PLAYING WITH ISOMETRIES
It is trust in life,
to compete with the impossible.
Panait ISTRATI
To reach the inaccessible star, this is my quest.
Jacques BREL
 e cannot go beyond the limits of the possible, but we can push
them forward. To do this, what can we do? For example, have we the ability to alter or add isometries on basic polygons? The answer is yes. We then get super-tiles with
amazing features.
e cannot go beyond the limits of the possible, but we can push
them forward. To do this, what can we do? For example, have we the ability to alter or add isometries on basic polygons? The answer is yes. We then get super-tiles with
amazing features.
• Let us take the 3a base polygon:
Let us add the isometries of the base polygon 1Gb, that is to say two glide reflections. We then get the next polygon:
On a rhomb we have two different isometries of rotation order 3.
Let us draw a motif according to this polygon. For example this "Li'l Wolf" opposite. He looks astounded because he comes to realize that he could
tessellate the plane not only according to types 3a and 1Gb, but also in many other ways.

Type 3a tessellation:
Tile type 2c divided into two identical motifs

Tile type 2Ge divided into two identical motifs
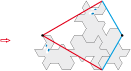
Tile type 6c divided into two identical motifs
Type 1Gb tessellation:

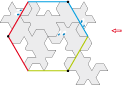
Tile type 3b divided into three identical motifs
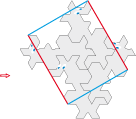
Tile type 1a divided into four identical motifs
• Now let us take the 6a base polygon. There we have an equilateral triangle with an isometry of rotation order 6 and one of rotation order 2:
For example this fish:

From this fish, we can, of course, make a tessellation of type 6a:

Then draw a pattern so that each side of the rotation order 2 be the reduction by half of each compensated deformation of the rotation order 6:

But we can also join to him three smaller identical fishes:
In this way, this gives us a type 6d tile divided into four:
But that is not all.
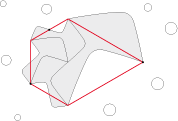
Let us take again our fish and let him be rotated 6 times. We can add all around a ring of smaller fishes. Then again, add a ring of even
smaller fishes, and so on to infinity.
We then get a perfectly hexagonal figure.
• In a way reminiscent of the example above, but with a different result, let us take a kite of type 6c:
Type 6c tessellation:

Let us draw a motif so that both sides of the order 3 rotation are equal to the sides of the order 6 rotation by the tangent of 30° (0.5774). For example this butterfly:
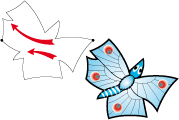
Type 6d tessellation:
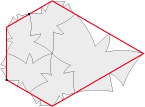
We can make a tessellation of type 6c but also of type 6d If we add four small butterflies as below:
To construct the Butterfly flake below, we have to make an order 6 rotation. And then, on the periphery, add a ring of small butterflies four times
more numerous. Then to this new periphery, make the same three times.
We can, of course, continue to add rings to infinity. Each new ring then, will generate more and
more points of infinity as below. All in all… we get an infinity of infinities.
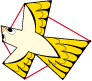
• As for the butterfly, but reversing the sides of the order 3 rotation, we can make this bird:
Here it is below by limiting to the fifth crown
• Let us take the 4S base polygon, that is to say a square with two symmetrical rotations of order 4. Let us add it four rotations of order 2:
Let us draw, for example, this bird:

We can tessellate the plane according to different types or make a rose or a non-periodic tessellation such the lowest one. We see a teeming mass of birds amongst which some go right their way and a few rarer, illuminate the four horizons.
• Let us see if we can draw a motif which has several base tiles:
This "Good Doggie" will do the trick:

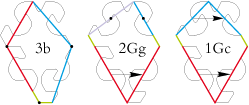
Type 3b tessellation:
Type 2Gg tessellation:
Type 1Gc tessellation:
Rose :



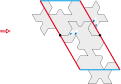
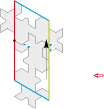
• And if we find again our lizard friends. In the Smaller and Smaller print (N°35), escher has used an isosceles right triangle of type 4a to reduce the lizards to infinity according to the diagram below:
This allows us to draw two lizards by triangle instead of one:
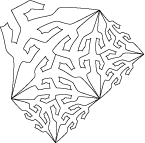
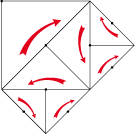
We can now make a order 4 rotation and reduce the lizards to infinity. The most direct way results an octogon.
In fact, there is not only a couple of different lizards, but four. This allows adaptations.
escher, in Smaller and Smaller, drew nine different lizards.
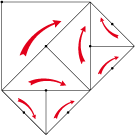
Let us invert the direction
of triangles as follows:
I hope you had lots of fun watching this method. This will be the final word: FIN (the END in French).
Return to summary
Nota bene :
If you liked this method,
a little word in the "Guestbook"
would make me happy.


















































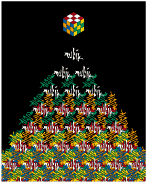






























 NICOLAS 2014
NICOLAS 2014
